Per capire bene le opzioni (e questo articolo 🙂 ) ti consiglio di leggere anche questi due articoli:
L’opzione è un contratto in base al quale l’aquirente (buyer), detto anche proponente (holder), acquisisce dal venditore (seller), detto anche sottoscrittore (writer), dietro corresponsione di un premio (valore o prezzo dell’opzione), il diritto di vendere (opzione put) o acquistare (azione call) a un prezzo prefissato, il prezzo di esercizio (strike price o exerecise price), detto anche prezzo base, un certo bene, detto attività sottostante (o più semplicemente sottostante), che può essere costituito sia da attività finanziarie sia da beni reali.
L’attività sottostante deve avere un mercato con quotazioni ufficiali e pubblicamente riconosciute; tipicamente, le opzioni vengono costruite su titoli, valute, tassi di interesse, merce e futures.
Inoltre, il suddetto diritto di acquistare o vendere (l’opzione) può essere esercitato entro una determinata data, e in questo caso si parla di opzioni di tipo americano, oppure solo alla scadenza, e in questo caso di parla di opzioni di tipo europeo.
“Recap”…
Americano –> puoi esercitare il diritto di acquistare e vendere sempre
Europeo –> puoi esercitare il diritto di acquistare e vendere solo alla scadenza
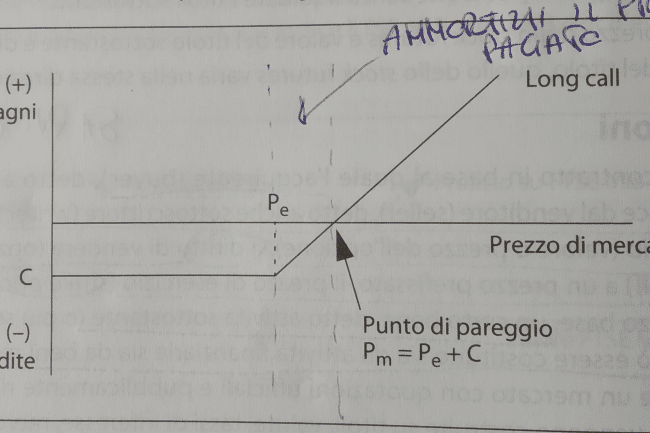
Buyer Call–> acquisisce il diritto ad acquistare l’attività sottostante il contratto
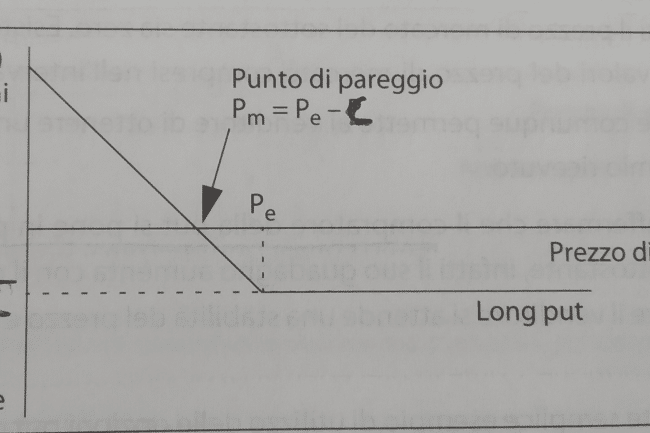
Buyer put –> acquisisce il diritto di vendere l’attività sottostante il contratto
il Writer –> assume l’obbligo su eventuale richiesta del buyer di vendere l’attività sottostante il contratto in caso di call option. Oppure di acquistarla in caso di put option.
N.B. il buyer acquisisce il diritto di comprare o vendere (può scegliere se comprare o se vendere) il writer invece assume l’obbligo di soddisfare la scelta del buyer. Ossia il writer ha l’obbligo di vendere se il buyer esercita la call, e ha l’obbligo di acquistare se il buyer esercita la put.
il buyer se sceglie di non esercitare il suo diritto, perde solo il premio. (mal che vada, se l’operazione va male il buyer perde solo il premio)
il writer invece essendo soggetto al volere del buyer, può registrare un profitto che nei migliori dei casi è pari al premio (è la perdita del buyer) mentre nel caso di opzioni call può incorrere in perdite dall’ammontare teoricamente illimitato. (scopri perché nell’articolo riservato alle Call)
Per calcolare l’utile derivante dall’esercizio di un’opzione è necessario considerare anche l’esborso costituito dal premio, il quale è tanto maggiore quanto più lontana è la scadenza del contratto e quanto più il prezzo di mercato è superiore (nel caso di una call) o inferiore (nel caso di una put) allo strike price.
quindi il premio è alto se:
- la scadenza è lunga
- se il prezzo di mercato è superiore allo strike price (nel caso di una call)
- se il prezzo di mercato è inferiore allo strike price (nel caso di una put)
Variabili che influenzano il prezzo di un’opzione e i coefficienti di sensibilità le greche
Quali sono le variabili che influenzano il prezzo di un’opzione?
- scadenza: più è lontana più è elevato il valore dell’opzione, poiché vi sono maggiori probabilità che alla scadenza l’opzione abbia un valore intrinseco positivo, e maggiore sarà il premio da dover pagare;
- volatilità del sottostante: più è elevata la variabilità del prezzo del sottostante, maggiore è il premio da pagare per l’opzione. Le opzioni di tipo americano, in particolare hanno un prezzo più alto, perché consentono di sfruttare in ogni momento le variazioni favorevoli di prezzo;
- dividendi distribuiti dal sottostante: maggiore è il dividendo distribuito, più si riduce il valore dell’azione sottostante, pertanto l’opzione call vedrà ridurre il suo valore e l’opzione put vedrà incrementare il suo valore.
- differenza tra il prezzo di mercato del sottostante e prezzo strike: al crescere di questa differenza, aumenta il valore dell’opzione
- Livello di tasso d’interesse: all’aumentare del tasso d’interesse aumenta il valore dell’opzione call, poiché aumenta la convenienza dell’acquisto dell’opzione per controllare l’azione sottostante piuttosto che acquistare l’azione, prendendo a prestito risorse finanziarie ad un tasso elevato. Al contrario all’aumentare del tasso di interesse, si riduce il valore della put, poiché conviene vendere a pronti il sottostante e impiegare il ricavato al tasso di mercato, piuttosto che venderlo a termine. In altri termini, in regime di elevati tassi di mercato, non conviene attendere la scadenza di un’opzione per vendere l’azione sottostante, ma conviene vendere azioni per impiegare il capitale ottenuto, sfruttando l’elevato livello del tasso d’interesse.
- Aspettative degli operatori: se si attende un rialzo del titolo, e se nel contempo si desidera limitare la perdita massima e/o non si hanno capitali sufficienti ad acquistare il titolo sottostante, conviene acquistare una call o vendere una put; se al contrario si attende un ribasso del titolo e se nel contempo si desidera limitare la perdita massima, e si intende proteggere il proprio portafoglio da un ribasso dei prezzi, conviene acquistare una put o vendere una call; se infine le attese sono quelle di stabilità del titolo sottostante, o se si vuole generare un reddito addizionale, conviene vendere una call o una put.
| fattori | opzione call | opzione put |
| prezzo del sottostante | relazione diretta con il premio (all’aumentare del prezzo del sottostante, il premio della call aumenta e viceversa) | relazione inversa con il premio |
| prezzo strike | relazione inversa | relazione diretta |
| volatilità | relazione diretta | relazione diretta |
| tempo a scadenza | relazione diretta | relazione diretta |
| tassi d’interesse | relazione diretta | relazione inversa |
| dividendi | relazione inversa | relazione diretta |
Per quanto riguarda le prime due variabili (prezzo di esercizio e prezzo di mercato) la relazione è diversa a seconda che si tratti di un opzione call o di una put. Nel caso di una call a parità di altre condizioni l’opzione ha un valore tanto maggiore quanto minore è il prezzo di esercizio, semplicemente perché attribuisce al compratore il diritto di acquistare a un prezzo inferiore.
Al contrario, un’opzione put ha un valore tanto maggiore quanto maggiore è il prezzo di esercizio. Ciò in quanto a parità di altre condizioni, un prezzo di esercizio maggiore implica il diritto di vendere a un prezzo più elevato.
Per il prezzo di mercato vale naturalmente la relazione opposta: un’opzione call aumenta di valore al crescere del prezzo di mercato e viceversaper la put. Al crescere del prezzo di mercato, infatti, il diritto di acquistare a un prezzo predeterminato aumenta di valore mentre il diritto di vendere a un prezzo prefissato diminuisce di valore.
In generale ogni opzione ha un valore che risulta tanto maggiore quanto maggiore è la vita residua e quanto maggiore è la volatilità. Infatti le opzioni sono in qualche modo assimilabili a dei contratti di assicurazione e dunque hanno un valore/costo tanto maggiore quanto maggiore è il tempo (la durata della polizza) e quanto maggiore è il rischio (volatilità). Questa relazione positiva vale dunque sia per le opzioni call che per le opzioni put.
Per ciò che concerne il tasso di interesse a breve termine la relazione non è immediata. Ciò in quanto un aumento del tasso privo di rischio fa aumentare da un lato il tasso atteso di rendimento del sottostante e dunque il prezzo a termine dell’attività sottostante, dall’altro fa diminuire il valore attuale dei guadagni futuri connessi all’eventuale esercizio dell’opzione.
Entrambi questi effetti si riverbano negativamente sul valore della put, che quindi diminuisce all’aumentare dei tassi. Nel caso della call succede invece che il primo effetto ha valenza positiva sul valore dell’opzione mentre il secondo negativa. Si può comunque dimostrare che il primo effetto è dominante per cui il valore della call aumenta all’aumentare dei tassi. Le relazioni menzionate sono sinteticamente riportate nella seguente tabella.
| | call | put |
| prezzo di esercizio | – | + |
| prezzo di mercato | + | – |
| vita residua | + | + |
| volatilità | + | + |
| tasso di interesse | + | – |
Un altro fattore potenzialmente in grado di influire anche se indirettamente sul valore dell’opzione è lo stacco dei dividendi; i dividendi infatti deprimono il prezzo delle azioni in misura maggiore quanto più sono ingenti. Pertanto possiamo attribuire alla distribuzione di dividendi un effetto negativo sul valore della call e un effetto positivo su quello di una put, anche se tali effetti sono già considerati dal prezzo di mercato del sottostante.
la sensibilità del valore di un opzione al variare delle sue determinanti
La sensibilità del valore di un’opzione al variare delle sue determinanti viene generalmente misurata facendo ricorso a dei coefficienti, detti anche “greche” delle opzioni, che esprimono in modo sintetico la variazione che il valore dell’opzione subirebbe se uno dei fattori sopra considerati variasse di un’unità.
- Delta; Il più importante di questi coefficienti è il delta di un’opzione. Esso misura la variazione che il valore di un’opzione subirebbe se il prezzo dell’attività sottostante variasse di un’unità. Le opzioni call hanno delta positivo: al crescere del prezzo di mercato, infatti, il valore di una call aumenta. Al contrario, le opzioni put hanno delta negativo: un aumento del prezzo di mercato dell’attività sottostante provoca infatti una diminuzione del valore di una put.
- Vega; misura la sensibilità di un’opzione al variare della volatilità dell’attività sottostante. Tutte le opzioni, siano esse call o put hanno vega positivo, in quanto un aumento della volatilità determina sempre, a parità di altre condizioni, un aumento del valore dell’opzione.
- Gamma; Misura la variazione del delta di un’opzione al variare del prezzo dell’attività sottostante. è infatti noto che la sensibilità di un’opzione al prezzo dell’underlying non è costante ma varia al variare del prezzo dell’attività sottostante.
- Theta; Esso misura la sensibilità di un’opzione al variare della sua vita residua, ossia al trascorrere del tempo. Poiché infatti ogni opzione ha un valore che è tanto maggiore quanto maggiore è la sua vita residua, il semplice passaggio del tempo determina una diminuzione del valore dell’opzione. Questo fenomeno , detto time decay, è tanto più significativo quanto maggiore è il theta di un’opzione.
- Rho; Misura la sensibilità del valore di un’opzione al variare del tasso di interesse a breve. In altri termini, esso indica la variazione che il prezzo dell’opzione subisce in corrispondenza di una variazione unitaria dei tassi di interesse di mercato.
| Greek | Misura… |
| delta | … la sensibilità del prezzo del derivato rispetto al prezzo del sottostante (e indica anche la posizione in titoli equivalente) |
| gamma | … la sensibilità di delta rispetto al prezzo di mercato del sottostante |
| rho | … la sensibilità del prezzo del derivato ai tassi d’interesse di mercato |
| theta | … la sensibilità del prezzo del derivato al trascorrere del tempo |
| vega | … la sensibilità del prezzo del derivato alla volatilità del sottostante |