Oggi parliamo della teoria di portafoglio di Markowitz , utilizzata per costruire portafogli di attività rischiose.
Per portafoglio si intende un insieme di attività finanziarie in cui ciascun attività è inserita con una certa porzione o peso rispetto al totale della ricchezza investita.
Gli investitori valutano e selezionano i portafogli su cui investire in funzione di due paramentri:
– rendimento, o meglio rendimento atteso e si indica con E(R) che indica la variabile casuale rendimento atteso
– rischio, che si calcola in termini di varianza dei rendimenti, e si indica con
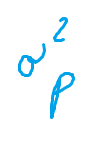
o anche in termini di deviazione standard, pari alla radice quadrata della varianza e si indica con
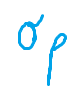
Il rendimento e il rischio di un portafoglio sono funzioni di rendimento e rischio delle singole attività che lo compongono. Infatti, il rendimento del portafoglio altro non è che la media ponderata dei rendimenti dei titoli inseriti in portafoglio.
Il rischio del portafoglio è invece in genere inferiore alla media dei rischi dei titoli inseriti in portafoglio grazie al beneficio della diversificazione: infatti il rischio è tanto minore quanto minore è la volatilità dei rendimenti dei titoli che lo compongono e quanto minore è il grado di correlazione fra tali rendimenti, espresso dal coefficiente di correlazione che rappresenta il legame tra la variazione del rendimento di un titolo al variare del secondo titolo e viceversa.
Per semplificare, consideriamo il rendimento atteso e varianza di un portafoglio composto da due soli titoli, A e B, che sono dati rispettivamente da:
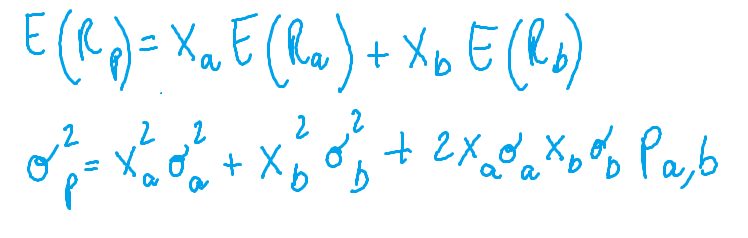
dove:
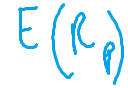
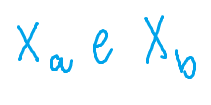
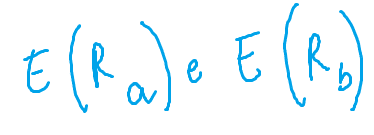
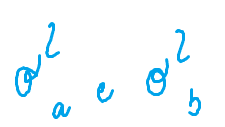
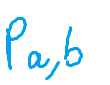
Il coefficiente di correlazione assume valori compresi tra -1 e +1 e quindi è possibile affermare che:
– se Corr(A,B) > 0 allora A e B sono positivamente correlati;
– se Corr(A,B) < 0 allora A e B sono negativamente correlati;
– se Corr(A,B) = 0 allora A e B sono incorrelati.
Consideriamo i seguenti tre casi:
- r(a,b) = 0: abbiamo situazione di indipendenza dei rendimenti dei due titoli, ossia la correlazione è nulla; la formula 2) diviene quindi:
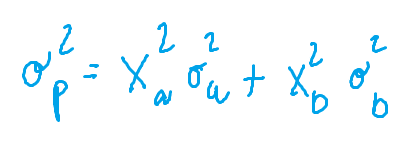
- r(a,b) = +1: abbiamo correlazione positiva perfetta. La varianza del portafoglio è pari alla media ponderata delle varianze dei due titoli e non si ha nessun beneficio dalla diversificazione: tutte le volte che la correlazione fra i titoli di un portafoglio è inferiore all’unità, ossia è imperfetta, la diversificazione è in grado di ridurre il rischio, dunque il rischio del portafoglio è inferiore a quello medio dei titoli che lo compongono. La formula 2) diventa quindi
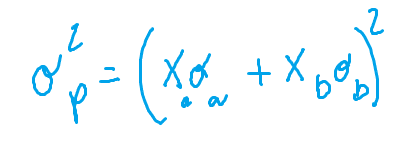
- r(a,b) = -1: abbiamo correlazione negativa perfetta. Si ottiene il massimo beneficio dalla diversificazione poiché i rendimenti si muovono in modo esattamente opposto; la formula 2) diventa quindi:
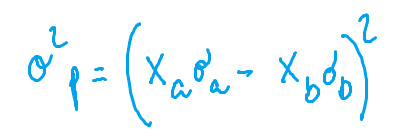
Una volta che per ogni portafoglio abbiamo calcolato deviazione standard e rendimento atteso possiamo effettuare un confronto per scegliere i portafogli migliori. Per effettuare questa scelta ci è di aiuto la costruzione della frontiera efficiente.
Individuiamo nel piano rischio-rendimento ( deviazione standard-rendimento atteso) tutti i portafogli che possiamo costruire dato un insieme di titoli, avremo che la frontiera efficiente è l’insieme dei portafogli posti lungo una curva, denominata appunto frontiera, che per un determinato rendimento hanno minor rischio e, per un certo grado di rischio, hanno maggior rendimento.
Tutti i portafogli collocati sotto la frontiera sono inefficienti, in quanto esisterà sempre un portafoglio migliore a parità rischio e uno migliore a parità di rendimento.

I portafogli posti sulla frontiera efficiente sono quindi l’insieme delle migliori combinazioni rischio-rendimento. Da questo insieme dobbiamo trovare il portafoglio ottimo, cioè quello che soddisfa il profilo del singolo investitore.
Per fare ciò bisogna definire l’atteggiamento verso il rischio del singolo investitore ricorrendo al concetto di curva di indifferenza. In base al grado di avversione al rischio possiamo ottenere una serie di curve di indifferenza che rappresentano le preferenze degli investitori in funzione del rendimento atteso e del rischio.
Una curva di indifferenza unisce tutti i portafogli che assicurano agli investitori la stessa utilità, cioè gli investitori esprimono la stessa preferenza per tutte le combinazioni di rischio-rendimento poste sulla curva.
Le curve di indifferenza sono infinite e variabili, in quanto nello stesso tempo ogni investitore presenta una propria curva di indifferenza distintiva e lo stesso tipo di investitore presenta curve di indifferenza diverse nel corso del tempo, secondo l’evoluzione e cambiamento delle proprie preferenze.

In base alla propensione al rischio dell’investitore, il portafoglio ottimo si colloca più a destra o più a sinistra lungo la frontiera efficiente: se un investitore ha un’elevata avversione al rischio, può preferire un portafoglio a basso rischio che si colloca nella zona in basso a sinistra della frontiera efficiente, zona che presenta livelli di rischio bassi. Mentre invece un investitore più propenso al rischio preferisce un portafoglio aggressivo che si posiziona nella zona alta a destra della frontiera.

Possiamo concludere affermando che la migliore scelta di investimento per l’investitore, cioè il portafoglio ottimo, sarà quella corrispondente al punto di tangenza fra la curva d’indifferenza più alta e la frontiera efficiente.
P.s. Se hai bisogno di una consulenza io ci sono.
[ut_btn button_effect=”winona” button_border_radius=”18″ font_family=”inherit” font_weight=”” button_text=”Richiedi consulenza” button_link=”url:https%3A%2F%2Ffilippoangeloni.com%2Fconsulenza%2F||target:%20_blank|” button_text_color=”#ffffff”]




